Розділ 1. Арифметичні та логічні основи МП техніки

1 Системи числення

2 Перетворення чисел

3 Машинне слово

4 Додавання та віднімання двійкових чисел

5 Множення і ділення двійкових чисел з фіксованою комою

6 Логічні функції

7 Мінімізація логічних функцій. Карти Карно.

1 Системи числення

У цифровій техніці вся інформація незалежно від її характеру представляється в числовій формі, причому використовуються тільки позиційні системи числення. У цих системах будь-яке ціле позитивне n-розрядне число записується у вигляді послідовності n цифр X_n-1X_n-2..X₁X₀. Число a (0, 1, 2, ..., a - 1), приймається для представлення цифр, що визначають основу системи числення. Внесок цифри в число залежить як від цієї основи, так і від займаної нею позиції (розряду) у послідовності цифр. Цифра x_k входить з вагою a_k і означає x_ka_k, а вся послідовність цифр Х_n-1Х_n-2 ... X₁Х₀ виражає в системі числення з основою а число

x_n-1 a ^n-1+ x_n-2 a ^n-2+…+ x₁ a ¹+ x₀ a⁰.

Звична десяткова система (а = 10) використовує цифри 0, 1, 2, .... 9. Наприклад, 3175 = 3 * 10³+ 1 * 10²+ 7 * l0¹ + 5 * 10⁰. В обчислювальній техніці переважне значення отримала двійкова система числення, для якої використовуються цифри 0 і 1. Двійковий розряд, що представляє собою найменшу кількість інформації, називається бітом. Послідовність двійкових цифр Х_n-1Х_n-2 ... X₁Х₀ служить записом двійкового числа

x_n-1 2 ^n-1+ x_n-2 2 ^n-2+…+ x₁ 2 ¹+ x₀ 2⁰.

Серед інших систем числення найчастіше використовуються вісімкова і шістнадцяткова. У вісімковій системі цифри представляються тими ж символами, що й у десятковій, а в шістнадцатятковій системі до них додаються ще шість символів А, В, С, D, Е, F, що відповідають десятковим числам 10, 11, 12, 13, 14, 15. Якщо потрібно вказати основу системи числення, запис числа супроводжується десятковим індексом. Наприклад:

10110₂=(1*2⁴+1*2³+0*2²+1*2¹+0*2⁰) =26₁₀;

5327₈=(5*8³+3*8²+2*8¹+7*8⁰) =2775₁₀;

2DF9₈=(2*16³+13*16²+15*16¹+9*16⁰) =11769₁₀.

Для перетворення числа з будь-якої системи числення в десяткову досить обчислити значення відповідного багаточлена, підставивши в нього десяткові значення розрядів і основу системи числення. Обчислення зручно виконувати за схемою Горнера, заснованої на представленні багаточлена у виді

(…((x_n-1 a + x_n-2)a + x_n-3 )a + …+ x₁ )a+ x₀ a,

за допомогою яких здійснюються різні операції в десятковій і іншій системах числення .

У загальному випадку, коли число має дробову частину, остання відокремлюється від цілої часта розділовим символом – крапкою або комою:

n цифр цілої частини

m цифр дрібної частини

x_n-1 x_n-2 ... x₁ x₀, x_-1 x_-2 ... x_-m ,

що відповідає числу :

x_n-1 a ^n-1+ x_n-2 a ^n-2+ x₁ a ¹+ x₀ a⁰+ x_-1 a ^-1+ x_-2 a ^-2+ x_-m a ^-m

Вираження будь-якого числа в десятковій системі зводиться до обчислення його багаточленного представлення, наприклад;

405,37₈= (4*8²+0*8¹+ 5 * 8°+ 3*8 ^-1+ 7 *8^-2)₁₀ = 261,140625₁₀.

Арифметичні операції над числами в будь-якій системі числення виконуються за такими правилам, що й у десятковій системі.

2 Перетворення чисел

Найчастіше необхідно переводити десяткові числа в двійкові і навпаки, що можна виконати за допомогою універсального алгоритму, який застосовується окремо для цілої і дробової частин. Переведення цілої частий десяткового числа в двійкову систему зводиться до запису в зворотному порядку залишків (0 чи 1), що одержані при діленні вихідного числа і кожної наступної частки на два. Дробова частина виходить з цілих частин (0 чи 1) при її послідовному множенні на два, причому таке множення продовжується до тих пір, поки дробова частина не буде дорівнювати 0 або буде отримана необхідна кількість знаків після розділової коми, наприклад, 26,3125₁₀= 11010,0101₂

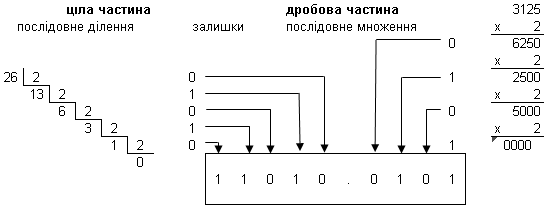
Рисунок 1 – Переведення десяткового числа в двійкове

Зворотне перетворення двійкового числа в десяткове можна виконати аналогічно з тим розходженням, що ділити і множити потрібно на 10 у двійковій системі, тобто на 1010₂ (рисунок 2). Як видно, при використанні такого алгоритму цифри десяткового еквівалента двійкового числа представляються спочатку в двійковій системі. Для кожного десяткового розряду відводяться чотири двійкових розряди (тетрада). Тоді двійково-десятковий запис числа має вид:

26,3125 = 0010 0110,0011 0001 0010 0101.

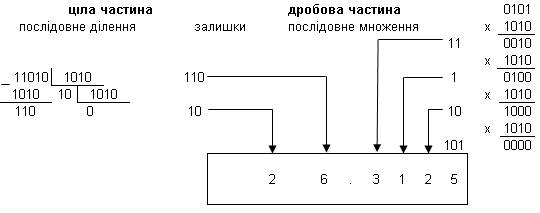
Рисунок 2 – Переведення двійкового числа в десяткове

Таке представлення чисел зручно при обробці в обчислювальних машинах інформації, що характеризується великою кількістю вихідних даних і результатів у десятковій системі числення.

Легше всього переводити в двійкові числа вісімкові та шістнадцяткові числа. Для цього необхідно кожен розряд вісімкового числа представити трійкою (тріадою), а шістнадцяткового – четвіркою (тетрадою) двійкових розрядів. Наприклад:

5327₈ = 101 011 010 111

2DF9₁₆ = 0010 1101 1111 1001

Зворотнє переведення двійкового числа у вісімкове або шістнадцяткове виконується розбиттям його на блоки (тріади або тетради) ліворуч та праворуч від розділового символу. Відсутні розряди в крайньому лівому і правому блоках доповнюються нулями. Потім кожна тріада заміняється вісімковим, а кожна тетрада шістнадцятковим числом. Наприклад:

1101010,11101 = 001 101 010,111 010 = 152,72₈

1101010,11101 = 0110 1010,1110 1000 = 5А,D8₁₆

Вісімкове та шістнадцяткове представлення двійкових чисел використовується для більш компактного запису при програмуванні і введенні програм в обчислювальні машини. Зокрема, шістнадцяткова система зручна для представлення байта інформації (8 біт), для цього достатньо двозначного шістнадцяткового числа.

3 Машинне слово

Сигнали, що грають роль носіїв інформації, представляються в цифрових системах послідовностями біт (байт), що поєднуються в слова. Довжина слова може бути будь-якою (від 4 до 128 біт). Цифрові сигнали можуть представлятися в двох формах: з фіксованої або з плаваючою комою. При представленні числа у формі з фіксованої комою n-розрядне слово розбивається на три частини. Перший біт використовується для знака (0 для позитивних чисел і 1 для негативних). Інші розряди розподіляються між цілою і дробовою частинами числа з твердим положенням місця розділення, тобто вказівкою кількості розрядів, що відводяться. Якщо для дробової частини виділено m біт, то найбільше по абсолютній величині число не може перевершувати (2_n-1-1)2^-m. Обмеження діапазону чисел, що представляються, і тверде розташування фіксованої коми – основні недоліки такого способу, що можуть привести до втрати точності при виконанні арифметичних операцій унаслідок переповнення.

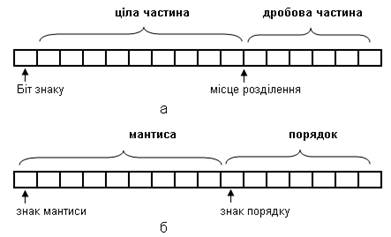
Рисунок 3 – Представлення чисел з фіксованою комою (а) та з плаваючою комою (б).

Більш зручною є форма з плаваючою комою. Вона заснована на співвідношенні N = М*2^E , де М – мантиса, E - порядок числа N. Величини М та Е можуть бути як позитивними, так і негативними, але М завжди дробове число, менше одиниці, а Е – ціле число. Обидві ці величини представляються як цілі числа і для кожного з них (включаючи знаки) приділяється в слові визначена кількість розрядів. При цьому розрядність мантиси впливає на точність, а розрядність порядку – на діапазон чисел, що представляються.

Зрушення мантиси на один розряд ліворуч збільшує, а праворуч – зменшує її вдвічі. Щоб такі зрушення не впливали на значення числа, необхідно зменшити або збільшити порядок на одиницю. Зрушення мантиси ліворуч допустимо тільки при наявності старшого нульового розряду. Якщо ж старший розряд дорівнює 1, то це відповідає максимально можливому значенню даної мантиси, що лежить у діапазоні 2^-1 <М< 1. Числа з таким представленням мантиси називають нормалізованими, і вони найчастіше використовуються в обчислювальних системах. Процес нормалізації складається в зрушенні числа на необхідну кількість розрядів ліворуч або праворуч з відповідним зменшенням або збільшенням порядку. Якщо мантиса і порядок нормалізованого числа, займають відповідно р и q розрядів, то мінімальне і максимальне значення (у десятковому записі) визначають діапазон представлення чисел Nmіn < N < Nmax

та .

У цьому відношенні форма з плаваючою комою краща.

При додаванні чисел з плаваючою комою, необхідно спочатку вирівняти показники доданків, для чого мантиса одного з них зрушується на число розрядів, рівне різниці показників. Множення зводиться до визначення добутку мантис і суми показників. Відповідні операції виконуються над цілими числами, а результат нормалізується.

4 Додавання та віднімання двійкових чисел

Додавання цілих багаторозрядних чисел у двійковій системі числення робиться порозрядно. У результаті додавання 1 + 1 одержуємо 10₂ = 2₁₀. Для представлення такого результату потрібно два розряди; при цьому з молодшого розряду в наступний, більш старший розряд, надходить одиниця переносу. Перенос додається до відповідного розряду чисел, що додаються (рисунок 4).

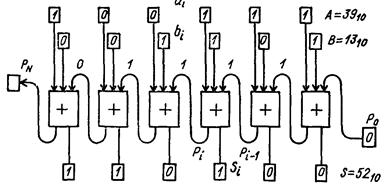
Рисунок 4 – Схема додавання цілих багато розрядних чисел

Додавання здійснюється послідовно, починаючи з молодшого розряду. У кожному розряді додаються значення трьох величин: розряду операнда а_і, розряду операнда b_і та переносу з попереднього розряду p_i-1. У результаті додавання в кожному розряді одержуємо дві величини: значення суми s_і, значення переносу в наступний, більш старший розряд p_і. У розглянутому прикладі при додавання чисел А = 39₁₀ = 100111₂ і В = 13₁₀ = 001101₂ отриманий результат S = 52₁₀ = 110100₂, який містить шість розрядів, тобто укладається в прийняту розрядну сітку. Додамо до отриманого результату 52₁₀ (110100₂) число 13₁₀ (011101₂):

	110100		52
+	001101	+	13
	1000001		65

У підсумку одержали число, що містить сім розрядів, старший з який відповідає розряду переносу, що знаходиться за межами розрядної сітки. Наявність одиниці в розряді переносу повідомляє про переповнення розрядної сітки.

Негативні числа можуть записуватися у виді прямих, зворотних або додаткових кодів. Знаковий розряд позитивних чисел дорівнює нулю, а негативних – одиниці, і відокремлюються від інших розрядів крапкою. Негативні числа переважно застосовуються у сучасних мікро-ЕОМ у додаткових кодах.

Операція одержання додаткового коду негативного числа з прямого коду називається операцією доповнення. Ця операція полягає в інвертуванні всіх розрядів вихідного коду (включаючи знаковий) і додаванні до молодшого розряду одиниці. Застосуємо операцію доповнення до прямого коду числа 0.110100₂ = + 52₁₀. Результат 1.001100 відповідає додатковому коду негативного числа -52₁₀. Якщо до цього результату ще раз застосувати операцію доповнення, то знову одержимо вихідний код 0.110100.

Таким чином, у системі двійкових чисел зі знаком заміна позитивного числа на рівне йому по модулю негативне і навпаки, негативного - на позитивне, здійснюється застосуванням до коду даного числа операції доповнення. Ця властивість представлення негативних чисел у додаткових кодах дозволяє при виконанні арифметичних операцій узагалі відмовитися від операції віднімання, замінивши її операцією додавання з числом, що має знак, протилежний знаку від'ємника.

Додавання двійкових чисел, представлених у формі з фіксованою комою, виконується аналогічно додаванню цілих чисел. Номера розрядів визначаються їх розташуванням у числі щодо коми, яка відокремлює цілу частину від дробової. Порядок додавання не залежить від розташування коми. Тому операцію додавання розглянемо на прикладі додавання цілих чисел.

Приклад 1. Додавання двох позитивних чисел:

	0,100111		39
+	0,001101	+	13
	0,110100		52

Результат не виходить за межі розрядної сітки і тому правильний.

Приклад 2. Додавання двох позитивних чисел:

	0,110111		52
+	0,001101	+	13
	1,000001	–	63

У результаті додавання вийшло негативне число –63, тобто результат додавання невірний, оскільки вірний результат + 65 виходить за межі розрядної сітки. Дійсно, прийнята розрядна сітка забезпечує представлення двійкових чисел у межах від 1.000000₂ = – 64₁₀ до 0.111111₂ = +63₁₀, а отримана сума + 65 перебуває за її межами.

Приклад 3. Додавання двох чисел з різними знаками:

	1,001100	–	52
+	0,001101	+	13
	1,011001	–	39

Результат додавання вірний і має знак більшого по модулю числа. При додаванні чисел з різними знаками модуль результату завжди не перевищує модуля кожного з вихідних операндів. Тому переповнення розрядної сітки неможливо.

Приклад 4. Додавання двох чисел, рівних по модулі і різних за знаком:

	1,011001	–	39
+	0,100111	+	39
	10,000000		0

Результат додавання вірний, якщо ігнорувати одиницю в розряді переповнення, розташованому за межами розрядної сітки.

Приклад 5. Додавання двох негативних чисел.

	1,011001	–	39
+	1,110011	–	13
	11,001100	–	52

Сума знаходиться в межах розрядної сітки, тобто результат вірний, якщо зневажити одиницею в розряді переповнення.

Приклад 6. Додавання двох негативних чисел:

	1,001100	–	52
+	1,110011	–	13
	10111111	+	63

Сума перебуває за межами розрядної сітки, тобто результат невірний і має позитивний знак. Одиницею в розряді переповнення ігноруємо.

Розглянуті приклади підтверджують те, що при додаванні чисел зі знаком у додаткових кодах значенням розряду переповнення потрібно ігнорувати.

Можливі випадки одержання невірних результатів за умови, якщо числа, що додаються, мають однаковий знак, а знак суми - протилежний. Результат виконання операції додавання чисел повинний обов'язково перевірятись, щоб уникнути одержання невірного результату. Правило перевірки таке:

- якщо знак операндів однаковий, а знак суми йому протилежний, то результат буде некоректний;

- із всіх інших випадках результат додавання вірний.

Випадок, коли отриманий результат виходить за межі припустимого діапазону представлення чисел, називається переповненням розрядної сітки.

5 Множення і ділення двійкових чисел з фіксованою комою

Множення двійкових чисел виконують у прямому коді. Знак добутку визначають за знаковими розрядами множеного і множника у відповідності з таким правилом: якщо знак операндів однаковий, то знак добутку - позитивний; у противному випадку знак добутку негативний.

Знак добутку двох чисел не впливає на алгоритм виконання операції множення модулів цих чисел. Найпростішим способом множення є багаторазове додавання, що полягає в додаванні множеного самого із собою, причому число таких операцій дорівнює множнику. Такий алгоритм множення є простим, але повільним.

Часто використовують спосіб множення, процедура якого аналогічна процедурам множення вручну. У цьому випадку результат одержують додаванням часткових добутків, що є результатом множення множеного на значення чергових розрядів множника. Кожен частковий добуток удвічі перевищує попереднє значення, що відповідає зрушенню його ліворуч на один розряд. Наприклад:

	11012		1310
x	10112		1110
	1101		13
	1101	+	13
+	0000		143
	1101
	100011112

Характерно, що розрядність добутку двійкових чисел удвічі перевищує розрядність співмножників. Якщо в добутку беруть участь мантиси, тобто правильні дроби, то молодші розряди, що виходять за межі розрядної сітки, можуть бути відкинуті з врахуванням округлення або без.

Найбільшу швидкість множення одержують у статичних множних пристроях, практична реалізація яких можлива завдяки наявності спеціальних пристроїв, які запам'ятовують таблиці множення багаторозрядних чисел. Однак зі збільшенням розрядності співмножників складність таких пристроїв швидко зростає. Тому даний спосіб множення можливий лише для чисел з порівняно невеликою кількістю двійкових розрядів.

В універсальних обчислювальних машинах, як правило, реалізується "шкільний" алгоритм ділення чисел. "Шкільний" алгоритм ділення полягає в тому, що дільник на кожному кроці віднімається від діленого стільки разів (починаючи зі старших розрядів), скільки це можливо для отримання найменшого позитивного залишку. Тоді в черговий розряд частки записується цифра, що дорівнює числу дільників, що містяться в діленому на даному кроці. При діленні операцію віднімання повторюють до тих пір, поки ділене не стане менше дільника. Існують і інші алгоритми, наприклад, алгоритм ділення з відновленням залишку та алгоритм ділення без відновлення залишку.

6 Логічні функції

При проектуванні обчислювальної техніки для формального опису логічних схем використовують математичний апарат алгебри логіки, об’єктом дослідження якого є функції, які набувають, як і їх аргументи, тільки два значення – 0 та 1. Вивчення властивостей таких функцій є дуже важливим для успішного розв’язання задач, які виникають перед фахівцями з проектування засобів обчислювальної техніки.

Функцію f(x₁, x₂, ..., х_n), яка набуває тільки значення 0 або 1, як і її аргументи, прийнято називати логічною функцією або булевою функцією. Аргументи булевої функції також називають булевими.

Довільна булева функція задається одним із трьох способів: табличним, геометричним та аналітичним.

Оскільки аргументи логічних функцій можуть набувати лише двох значень, область визначення будь-якої логічної функції скінченна. Тому будь-яка функція алгебри логіки може бути задана таблицею її значень залежно від значень аргументів.

Таблиця 1 – Логічні функції

х1 х2	0 0 1 1 0 1 0 1	Позначення	Назва функції	Читання	Формула
Y0	0 0 0 0	0	Константа 0	будь-який 0	0
Y1	0 0 0 1	x1x2; x1^ x2	Кон’юнкція	x1 та x2	x1x2
Y2	0 0 1 0	x1¬x2	Заперечення імплікації	x1 але не x2
Y3	0 0 1 1	x1	Повторення x1	як x1	x1
Y4	0 1 0 0	x2 ¬ x1	Заперечення зворотної імплікації	х2, але не x1
Y5	0 1 0 1	x2	Повторення x2	як x2	x2
Y6	0 1 1 0	x1 Å x2	Сума по модуля 2	або x1 або x2	+
Y7	0 1 1 1	x1+x2, x1Úx2,	Дізюкція	x1 або x2	x1+x2
Y8	1 0 0 0	x1¯x2	Стрілка Пірса	не x1 не x2
Y9	1 0 0 1	x1~x2	Еквіваленція	x1 як x2	+ x1x2
Y10	1 0 1 0		Заперечення x2	не x2
Y11	1 0 1 1	x2 ® x1	Зворотна імплікація	якщо x2, то x1	x1+
Y12	1 1 0 0		Заперечення x1	не x1
Y13	1 1 0 1	x1 ® x2	Іплікація	якщо x1, то x2	+ x2
Y14	1 1 1 0	x1/x2	Штрих Шефера	не x1 або не x2	+
Y15	1 1 1 1	1	Константа 1	будь-яка 1	1

Логічні функції двох змінних наведені в таблиці 1 можливо розглядати як елементарні функції над однією, двома двійковими змінними. Шість з наведених функцій не залежать від х₁ або від х₂, або від обох разом: константи (Y₀ та Y₁₅), повторення (Y₃ та Y₅), заперечення (Y₁₀ та Y₁₂).

Серед інших 10 функцій (Y₄ та Y₁₁) відрізняються від (Y₂ та Y₁₃) тільки порядком розташування аргументів, тому серед 16 функцій двох змінних оригінальними є тільки 8: Y₁, Y₂, Y₆, Y₇, Y₈, Y₉, Y₁₃, Y₁₄.

Логічні функції, що наведені в таблиці 1, можна розглядати, як елементарні операції над однією або двома двійковими змінними, функціонально повна система таких операцій утворює на множині двохзначних змінних алгебру логіки. Найбільш розповсюдженою є булева алгебра, в якій як основні операції прийняті кон’юнкція х₁х₂ (І), диз’юнкція х₁+х₂ (АБО) та заперечення (НЕ).

Основні правила булевої алгебри наведені в таблиці 2.

Таблиця 2 – Основні правила булевої алгебри

Властивість	Перша форма	Друга форма
Комутативність	x + y = y + x	xy = yx
Асоціативність	x + (y + z) = (x + y) + z	x (yz) = (xy)z
Дистрибутивність	x(y + z) = xy + xz	x + yz = (x + y)(x + z)
Доповнення	x + = 1	x∙= 0
Повтор змінної	x + 0 = x	x + 1 = x
Повтор константи	x + 1 = 1	x ∙ 0 = 0
Подвійне заперечення	= x	= x
Ідемпотентність	x + x = x	x∙x = x
Загони де Моргана	=	= +
Склеювання	xy + x = x	(x+ y)(x + ) = x
Поглинання	x + xy = x	x(x + y) = x
Заміщення	x + y = x + y	x ( + y) = xy
Виявлення	xy + z = xy + z + yz	(x+y)(+z) = (x+y)(+z)(y+z)

7 Мінімізація логічних функцій. Карти Карно.

Карти Карно являють собою спеціально організовані таблиці відповідності, на котрих зручно здійснюються операції склеювання при спрощенні функції на шляху до мінімальних форм.

Одним з способів подання булевих функцій від невеликої кількості змінних є карти Карно. Їх різновид – карти (діаграми) Вейча, які будуються як розгортки кубів на площині. При цьому вершини куба зображуються як клітинки карти, координати яких збігаються з координатами відповідних вершин куба. Карта заповнюється так само, як таблиця істинності: значення 1 вказується в клітинці, що відповідає набору, на якому функція має значення 1. Значення 0 звичайно на картах не відображається.

Карти (діаграми) Вейча дозволяють швидко одержати мінімальні булевої функції f невеликої кількості змінних. В основі методу лежить задання булевих функцій діаграмами деякого спеціального вигляду: їх називають діаграми Вейча. Для булевої функції двох змінних діаграма Вейча має вигляд (рисунок 5, а). Кожна клітинка діаграми відповідає набору змінних булевої функції в її таблиці істинності. В клітинці діаграми Вейча ставиться одиниця, якщо булева функція набуває одиничного значення на відповідному наборі. Нульові значення булевої функції в діаграмі Вейча не проставляються. Для булевої функції трьох змінних діаграма Вейча має такий вигляд (рисунок 5, б), аналогічно діаграма Вейча для функції чотирьох змінних має вигляд (рисунок 5, в).

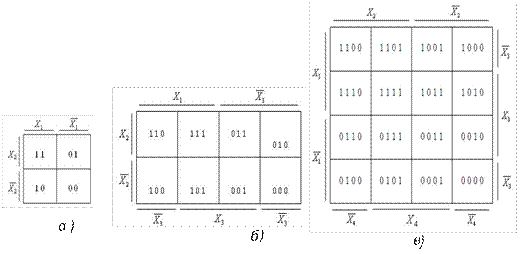
Рисунок 5 – Діаграма Вейча а) для двох змінних, б) для трьох змінних, в) для чотирьох змінних

Правила мінімізації такі:

1. Дві сусідні клітинки (два 0-куби) утворюють один 1-куб. При цьому мається на увазі, що клітинки, які знаходяться на межах карти, також є сусідніми відносно одна одної;

2. Чотири вершини можуть об’єднуватися, утворюючи один 2-куб, що містить дві незалежні координати;

3. Вісім вершин можуть об’єднуватися, утворюючи один 3-куб;

4. Шістнадцять вершин, об’єднуючись, утворюють один 4-куб і т.д.

Відзначимо, що сусідніми клітинками є клітинки, які збігаються при суміщенні карт поворотом навколо загального ребра. Сукупність прямокутників, які покривають усі одиниці, називається покриттям. Зазначимо, що одна і та ж комірка може покриватися два або декілька разів.

Таким чином, формула, що отримується в результаті мінімізації логічної функції за допомогою діаграм Вейча, містить суму стількох елементарних добутків, скільки прямокутників є в покритті. Чим більше комірок в прямокутнику, тим менше змінних міститься у відповідному йому елементарному добутку.

Нехай задана логічна функція:

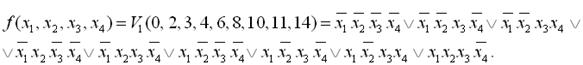
Будуємо діаграму Вейча для заданої функції:

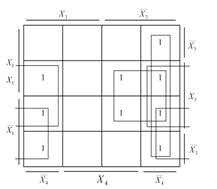
Рисунок 6 – Мінімізація логічної функції за допомогою діаграми Вейча

Таким чином, мінімальна форма заданої функції має такий вигляд:

Метод карт Карно знаходить широке застосування для мінімізації логічних функцій. Основою мінімізації за допомогою карти Карно є такий крок: два мінтерма, що знаходяться в сусідніх клітинках карти, можуть бути замінені однією кон’юнкцією, яка містить на одну змінну менше. Якщо сусідніми є дві пари мінтермів, то така група з чотирьох мінтермів може бути замінена кон’юнкцією, яка містить на дві змінних менше. В загальному випадку наявність мінтермів в 2n сусідніх клітинках дозволяє виключити n змінних. Такі дії можливо показати, якщо сусідні пари мінтермів перетворювати методом послідовного виключення змінних, використовуючи при цьому закони (x₁∨ x₂) x₃= x₁ x₃ ∨ x₂ x₃; (x₁ x₂) ∨ x₃=(x₁∨ x₃) (x₂∨ x₃),

правила поглинання x₁ ∨ x₁x₂ = x₁ і склеювання

x1 x2

∨

x1

x2

= x1;

(x1 ∨ x2)

(x1

∨

x2

) = x1

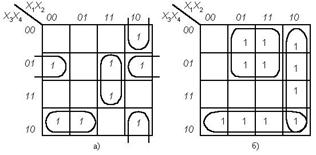
Рисунок 7 – Приклади об’єднання клітинок в картах Карно

Виконуючи мінімізацію необхідно пам’ятати, що сусідніми клітинками є не тільки клітинки, які розміщені близько по горизонталі і вертикалі, але й клітинки на протилежних сторонах карти Карно; клітинки можуть об’єднуватися по дві (рисунок 7, а), чотири (рисунок 7, б) і т. ін.; одна і та ж клітинка карти Карно може входити в декілька груп. Картами Карно можна користуватися для мінімізації логічних функцій.

Завдання 1. Спростити логічну функцію, що задана картою Карно. Побудувати схему, що реалізує таку функцію.

Завдання 2. Синтезувати у вигляді системи логічних рівнянь цифру 1 для світлодіодної матриці 5x7. Накреслити схему знакогенератора.

Синтезуємо у вигляді системи логічних рівнянь цифру 1 для світлодіодної матриці 5x7 (рисунок 8).

Таблиця 3 – Таблиця істинності знакогенератора

х2	х1	х0	Q4	Q3	Q2	Q1	Q0
0	0	0	0	0	0	1	0
0	0	1	0	0	1	1	0
0	1	0	0	1	0	1	0
0	1	1	0	0	0	1	0
1	0	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	1	0	0	0	1	1	1

Рисунок 8 – Зображення цифри 1 на світлодіодній матриці.

Запишемо систему логічних рівнянь, який описується п’ятирозрядний код, який знімається з виходу знакогенератора:

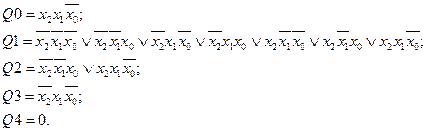
Отриману систему можна мінімізувати за допомогою карт Карно, які наведені на рисунку 9. Враховуючи, що комірка пам’яті з адресою 111 не використовується (позначено *), отримаємо мінімізований вираз:

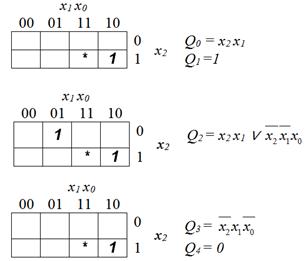
Рисунок 9 – Карти Карно для функцій Q₀, Q₂, Q₃.

За результатами мінімізації будується схема знакогенератора

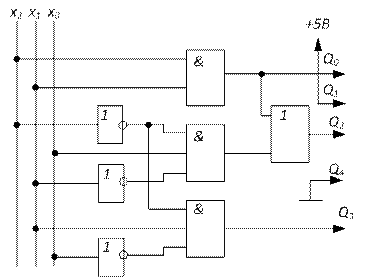
Рисунок 10 – Схема знакогенератора для реалізації цифри 1.

Завдання 3. Синтезувати у вигляді системи логічних рівнянь 2 букви (букву прізвища та імені) для світлодіодної матриці 7x9. Накреслити схему знакогенератора.

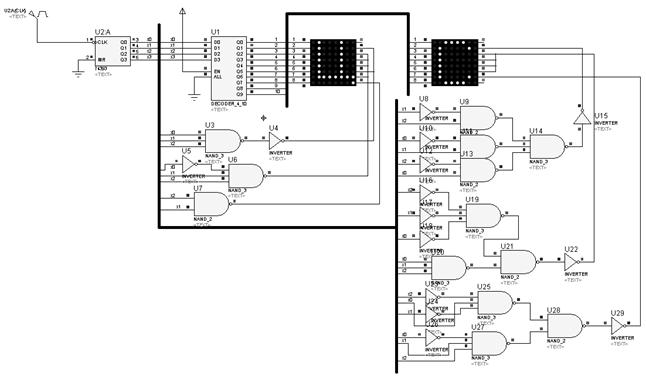
Рисунок 11 – Зразок виконання завдання 3 у середовищі Proteus

Завдання 4. Записати структурну формулу, яка реалізує комбінаційна схема, що наведена на рисунку 12. Спростити отриману структурну формулу і побудувати нову схему на елементах І, АБО та НЕ.

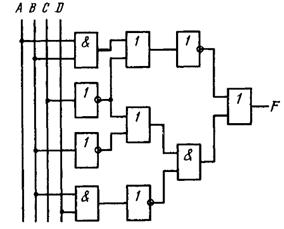
Рисунок 12 – Схема до завдання 4

Завдання 5. Синтезувати шифратор на п'ять входів (рисунок 13) а) на елементах АБО-НЕ; б) на елементах І-НЕ.

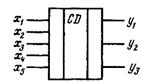
Рисунок 13 – Схема шифратора до завдання 5

Завдання 6. За принциповою електричною схемою (рисунок 14) провести аналіз і встановити функціональну залежність у вигляді формул алгебри логіки і таблиці істинності. За таблицею істинності скласти карти Карно, мінімізувати логічну функцію. Синтезувати комбінаційне пристрій у базисі І-НЕ, АБО-НЕ.

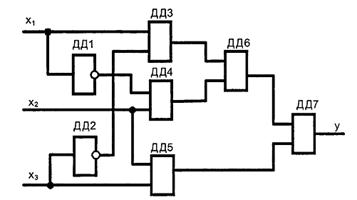
Рисунок 14 – Схема до завдання 6

ДД1, ДД2 – інвертори, знак «–» в таблице 4 означає, що елемент відсутній, знак «+» відповідає наявності інвертора в схемі

Таблиця 4 – Варіанти завдань

№	ДД1	ДД2	ДД3	ДД4	ДЦ5	ДД6	ДД7
1	+	-	и	АБО	І-НБ	АБО	І
2	-	+	АБО-НЕ	І-НЕ	АБО-НЕ	І	АБО
3	-	+	І	АБО	АБО-НЕ	І	АБО-НЕ
4	-	+	І-НЕ	АБО-НЕ	І-НЕ	АБО	І-НЕ
5	+	-	АБО	І	І-НЕ	АБО	І-НЕ
6	+	-	І-НЕ	І	АБО-НЕ	І	АБО-НЕ
7	_	+	АБО-НЕ	АБО	АБО	І-НЕ	І
8	+	-	І	І-НЕ	АБО-НЕ	І	АБО-НЕ
9	-	+	І-НЕ	І	І-НЕ	АБО	І-НЕ
10	+	-	АБО	І	АБО-НЕ	І	АБО-НЕ
11	+	-	АБО-НЕ	АБО	І-НЕ	АБО	І-НЕ
12	-	+	АБО НЕ	АБО	І	АБО-НЕ	АБО
ІЗ	-	+	АБО	І-НЕ	АБО	І-НЕ	І
14	-	+	АБО-НЕ	І-НЕ	АБО-НЕ	І	АБО-НЕ
15	+	-	І-НЕ	АБО	І	АБО-НЕ	АБО-НЕ
16	+	-	АБО-НЕ	І	АБО	І-НЕ	І
17	+	-	І	АБО	І-НЕ	АБО	І-НЕ
18	+	-	І-НЕ	І	АБО-НЕ	І	АБО
19	-	+	АБО-НЕ	І-НЕ	І	І	АБО
20	-	+	АБО-НЕ	АБО	АБО	І-НЕ	І-НЕ
21	+	-	І	І-НЕ	АБО	І-НЕ	І-НЕ
22	+	–	І-НЕ	АБО	І	АБО-НЕ	АБО-НЕ
23	-	+	АБО-НЕ	АБО	АБО	І-НЕ	І
24	-	+	І-НЕ	І	І-НЕ	АБО	І-НЕ
25	+	-	АБО	І-НЕ	І	АБО-НЕ	АБО
26	+	-	АБО-НЕ	АБО	АБО	І-НЕ	І-НЕ
27	-	+	І-НЕ	І	І	АБО-НЕ	АБО
28	+	-	АБО	АБО-НЕ	АБО-НЕ	І	АБО
29	-	+	І	АБО	І	АБО НЕ	АБО НЕ